Quantum mechanics is notoriously unintuitive and hard to understand. Prominent physicists such as Richard Feynman claimed that nobody, including himself, understands quantum mechanics - they just know how to compute things in order to get predictions that fit the facts. But does this model reflect the way nature really behaves or is it just a meaningless algorithm that happens to work? The problem with quantum mechanics is that if one tries to take seriously the model and say that its algorithm describes what really happens, one is lead to certain consequences very hard to accept - even the idea that death might not exist could be taken seriously.
Although we cannot (yet) say how the quantum mechanical formalism should be interpreted, we can pinpoint the reasons why it sounds so crazy. There are three main reasons: the typical theory of probability fails to give proper results at quantum level, rotation happens in a very unusual way, and the model uses a god's-eye view instead of a causal perspective. But first...
Quantum objects are particles, not waves
Besides the genuine weirdness of the quantum world there are also some additional artificial oddities introduced by a misleading presentation. One such misleading presentation is the idea that quantum objects are both particles and waves (some authors say neither particles nor waves). Actually, all experiments ever conducted point to the fact that quantum objects are particles. Nobody has ever observed any wave in quantum mechanics. The waves are used as a mathematical tool to describe the statistical motion of these particles - the wave formalism is the thing that replaces the traditional theory of probability. In the same way as in everyday life you cannot literally observe a probability, but just that various things happen one way or another with various frequencies, you cannot observe a wave in quantum mechanics (you just observe various things happening one way or another with various frequencies).
Experiments that showed that quantum objects are particles
There are two classic experiments that have shown first that light is emitted in "quanta of energy", i.e. as particles known as photons, and second that it is absorbed as "quanta of energy". The experiment about the emission of light involves the black body radiation and the explanation has been given by Planck. The experiment about the absorption of light involves the photoelectric effect and the explanation has been given by Einstein.
Suppose you have a box with mirror walls and that there is some light inside this box. If you make a tiny hole in the box some of the light will exit and you can thus observe it. The light inside the box has been emitted by the walls of the box - anything that has a certain temperature emits light. If the box is kept at a constant temperature the light inside the box will reach thermodynamic equilibrium - the same amount of light will be emitted by the walls and absorbed by them.
Not all the light in the box has the same wavelength. But some wavelengths are predominant. The image shows what wavelengths are predominant at various temperatures. As you can see, the box has to be quite hot (thousands of degrees) for the light to be predominantly in the visible part of the spectrum. (Incidentally, this curve can be used to determine the temperature of things based on the color of the light they emit.)
What Max Plank had observed was that this experimental graph flatly contradicted the thermodynamic theory of light available then. According to this theory light was a wave that could take any wavelength whatsoever. On the other hand according to thermodynamics the tendency toward equilibrium means that the energy tends to dissipate across all available "niches" (or degrees of freedom, as physicists call them). But if light could have any wavelength whatsoever, the tendency toward equilibrium would mean that all the possible wavelengths will tend to be equally represented.
That would mean for instance that when you were making that tiny hole in the box to see what kind of light is inside, or when you would look to any hot body for that matter, you would be irradiated, among other things, by x-rays and gamma rays - something that fortunately doesn't happen.
The only solution to this dilemma was to assume that light is emitted in quanta of energy, rather than in waves. Based on this idea, and using thermodynamics, Planck managed to compute the experimental graph of the black body radiation, and thus to explain why it has that shape.
Another related mystery has been that of the photoelectric effect. When one illuminates a piece of metal electrons come out of it. But the curious fact is this: the number of electrons coming out of the metal depends of the wavelength of the light. Moreover, there is a certain threshold. If the wavelength is to large no electrons would come out of the metal, no matter how much you increase the intensity of the incident light. This effect also contradicted classical electromagnetism.
Einstein explained it by using Plank's idea of quanta of energy. He assumed that all light comes in particles and the metal can either absorb the entire particle or not at all. The electrons inside the metal are held there with a certain force and an electron can be pulled out only if the energy of an incoming photon is sufficiently large. If you have a large number of photons (the intensity of light is large) but each photon has a small energy (the wavelength is large), no electron will be extracted. On the other hand if you increase the energy of each photon more and more electrons will be extracted, even if the intensity of the beam of light is small.
Such experiments showed that light is emitted as particles and it is absorbed as particles. But does it also travel as particles? For some time it seemed not. The following scenario seemed to describe what was happening: a particle of light is emitted, then the particle starts to expand as a wave (and has all the properties of waves), but finally when this wave reached something it suddenly collapses into a single point somewhere on the "wave front" and it is absorbed as a particle.
When this idea was popular Luis de Broglie proposed that electrons and all the other quantum objects also behave like light. This idea has obtained spectacular confirmation when physicists showed that electrons and neutrons also exhibit the properties traditionally associated with waves. One of the experimental techniques used for determining the 3D structure of crystals, neutron diffraction, is a direct consequence of this fact.
The idea of the collapse of the wave was seen as an oddity right from the start. Why would the wave front collapse into a particle? Moreover, is this collapse instantaneous? Wouldn't that contradict the theory of relativity? Niels Bohr argued that the collapse was caused by the act of observation itself and proposed that in quantum mechanics there is no longer a distinction between the thing observed and the observer. This is probably one of the most unfortunate ideas ever put forward in physics and many are still entangled in it. They wonder for example what exactly causes this supposed collapse of the wave: is it the consciousness of the observer or the contact to any "macroscopic object" (whatever that means)? Ideas such as the Schr?dinger cat were invented to emphasize the paradoxical consequences of Niels Bohr idea.
In reality there is no collapse because there is no wave. The particles travel as particles. There are many experiments that show this. One of the most famous is the Compton scattering. According to the wave theory of light when a beam of light hits an electron the emergent beam has the same wavelength as the initial beam. However, this is not what happens. There are two emergent beams - one that has the same initial wavelength and another one that has a larger wavelength (i.e. smaller energy). The image shows the Compton's experimental result. The angle phi is the angle between the incident beam of light and the emergent beam.
This experiment is easy to interpret if one considers that light hits the electron as a particle. In that case the Compton scattering simply describes an inelastic collision. Some of the incoming photons lose some of their energy during the collision. Some don't. This is why we get two beams. (It's impossible to determine which photon will scatter elastically or inelastically.) Using Niels Bohr's vision, one would have to say that the electron is the one that collapses the photon's wave function.
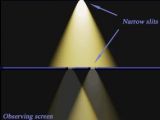
Another experiment is even more direct. Suppose you have a source of light, a wall with two tiny holes in it, very close to each other, and a screen behind the wall. This is a classic experimental set-up that reveals the interference of light (notice the pattern observed on the screen).
Apparently this experiment shows that the light reaches the wall with the two holes as a wave. This is because the observed pattern on the screen can be easily explained as the superposition of two waves each coming from each hole. According to this explanation the darker portions on the screen are where the maximum of one wave overlaps on the minimum of the other wave - and thus the two waves cancel each other; and the lighter portions are where either two maximums overlap or two minimums overlap - and thus the two waves reinforce each other.
But suppose we want to be sure that each photon passes through both holes. First of all we diminish the intensity of the beam of light - until we are sending one single photon after the other. Each photon hits the screen in a specific point - neither produces the interference patter alone. But when many photons have been sent the interference pattern is recreated.
Now we are adding behind the wall with two holes a divergent lens. The lens is added so the wall will be in its focal point. If the lens is sufficiently powerful the interference pattern disappears and one simply sees on the screen the distinct images of the two holes - separated from one another. In other words, it is as if the two holes were too distant from one another.
The interesting thing is that as the photons are sent one by one, they each end up either in one area of light or in the other one. It never happens that a photon will be half in one area and half in the other area. Due to the fact that these areas of light are the images of the holes it means that the photons either pass through one hole or through the other hole - they don't pass through both holes, as the wave theory assumes.
The thing is: the divergent lens destroys the interference pattern. But it doesn't do it by messing up with the photons before they pass through the double slits or while they are passing - the photons pass through the lens after they have already passed through the wall. So, the lens just revels what the photons have done - they have either passed through one hole or through the other hole, never through both.
Other more complicated experiments using beam splitters have also revealed the same thing: light is not only emitted and absorbed as a particle, but it also travels as a particle.
Beyond classical theory of probability
Once one understands that quantum things don't travel as waves one needs to reinterpret the wave formalism. That formalism simply describes how one computes probabilities in quantum mechanics. Richard Feynman has redescribed it in the following way:
A photon that goes from A to B can follow many possible trajectories. One should not have any a priori bias toward one particular trajectory (neither is "more plausible"). The quantum mechanical formalism that computes the probability that the particle goes from A to B is this: The particle is split into many "ghosts" each of which is sent on one of the possible trajectories. Each ghost has a watch with a single hand, called "probability amplitude". The speed by which this probability amplitude rotates is given by the energy of the photon. When a ghost reaches the final destination B its watch stops. Eventually all the ghosts reach B and get superimposed on each other. They compare their watches. Each points into a different direction. So, to compute the probability that the particle goes from A to B one adds up together all these probability amplitudes and gets a resultant arrow - the size of this arrow is the probability. The image shows an example - the red arrows are the ghosts' probability amplitudes in their final orientations and the blue arrow is the resultant probability amplitude (notice that all the red arrows have the same length - i.e. all the possibilities are taken to be equally probable).
The probability amplitude of one ghost can happen to be in the exact opposite direction of the probability amplitude of a different ghost. Thus these two amplitudes cancel each other - this is the equivalent of when the minimum of a wave overlaps on the maximum of another wave. In that case we can say that those trajectories on which these ghosts have traveled are virtually impossible. The actual trajectory is that which is not canceled. The probability amplitudes of some ghosts reinforce each other rather than canceling.
This formalism is simply the way quantum mechanics is done. But, as Fyenman noted, nobody understands why it works or what its significance is. Much of the puzzlement surrounding quantum mechanics stems from the oddity of this formalism. (Initially it had some sense, because people thought in terms of waves, but as we have seen, there are no real waves in quantum mechanics.)
This formalism also contradicts the classical theory of probability. In the classical theory of probability if something can happen in one way or another (the photon can pass through one hole or another) the probability of either 1 or 2 is the sum between probability of 1 and the probability of 2. But, as we have seen, it is possible that the actual result of such a combination is zero: some portions of the screen might be illuminated when only one hole is open and then become dark when the other hole is opened! The superposition of two light sources can lead to zero illumination in some places.
Spin
In our everyday world, we are accustomed to the following fact: When something is rotated by 360 degrees (or if we rotated by 360 degreed around an object) it returns to its initial position. After rotating by 360 degrees you will be looking in the same direction. What can be crazier than the failure of this simple fact?
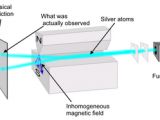
In 1922 Stern and Gerlach sent a beam of silver atoms through an inhomogeneous magnetic field (image). To understand this experiment you need to know that a rotating electric charge causes a magnetic field. Even a particle that is electrically neutral overall (such as an atom or a neutron) but which is composed of several rotating charges will exhibit a "magnetic momentum". So, Stern and Gerlach though about using this phenomenon to test whether the quantum particles spin. They used neutral atoms because they wanted to examine this phenomenon alone apart from other interactions of the magnetic field and electric charges. They obtained more than they were bargaining for!
They used an inhomogeneous external magnetic field to change the path of the particles. The magnetic field interacts with the intrinsic magnetic field produced by the particles' spin and changes their motion. One has to use an inhomogeneous magnetic field rather than a homogenous one because if the field would be symmetric the effects from one direction would cancel with effects from the opposite direction.
If the electrons inside the silver atoms would have rotated like any object we know, the beam of silver atoms would have been deflected to a certain degree away from the straight path. To what degree? Assuming that the intrinsic rotation is at random the particles should have been deflected to various angles. Thus a stripe of silver atoms should have accumulated on the screen. But this isn't what actually happens. The experimental result is that the beam is split in two beams each slightly deflected in one direction. In other words the particles (in this case the electrons inside the silver atoms) only rotate in two possible ways.
We can change the direction of the external magnetic field and the location of the two silver spots on the screen changes - but they always remain two spots and we never observe a whole stripe. This already shows that there is something seriously weird about how quantum objects spin and about how their spinning is influenced by the experimental set-up. It seems that the external magnetic field fixes their axis of rotation and that than the electrons can spin in only two ways (either clockwise or counterclockwise).
But things get weirder. Isidor Rabi used a more complex Ster-Gerlach apparatus that allowed him to rotate the external field. He found that he could change a particle from one state of spin to the other. But to do this he had to rotate the external field by 360 degrees. However, rotating the universe around a particle is equivalent to rotating the particle while keeping the universe at rest. So this rotation of the external field is in fact equivalent to the rotation of the particle. Do you get it? By rotating the electron by 360 degrees it switches to the other state of spin - instead of ending up exactly as it were, like all of us do when we spin around by 360 degrees.
In practical terms this also means that one can have two electrons occupying the same position is space (for instance the same orbit in an atom) as long as one has a certain spin and another has the other spin. It is as is space itself is folded in two and as a particle spins by 360 degrees it gets from one fold to the other one. (Read about how this impacts the phenomenon of superfluidity and superconductivity.)
The quantum mechanical god's eye view
I have already noted above that the quantum mechanical formalism is a means of computing the probability that something goes from A to B. However, quantum mechanics doesn't say anything about how the thing actually gets from A to B. In Newtonian mechanics for example one has the force that changes the body's velocity, so you can tell why the thing went in that direction rather than in some other direction. But in quantum mechanics things are presented as if the particles have some sort of premonition of where they will end up.
There is a good historic reason for why quantum mechanics is like this. In the 19th century the mathematician William Rowan Hamilton recreated the entire Newtonian mechanics in a novel way (he had some notable predecessors such as Lagrange and Euler). He assumed that everything that happens in nature happens as such that some thing, called action, is minimum. He discovered the most general formula for the action and described the entire field of mechanics this way.
He was saying something like: The particle goes from A to B in this amount of time. There are innumerable possible trajectories - which one would the particle "choose"? And he answered: the trajectory that corresponds to the minimum action. The simplest case is optics. In optics the action is the time - light goes on that path that takes the least amount of time. (Read more.)
You can see the similarity with the quantum mechanical approach. In fact it should be no surprise. Quantum mechanics was actually developed by changing the Hamiltonian approach to mechanics (it is no wonder that everything in quantum mechanics revolves around something called "hamiltonian"). The historic development was not at all straightforward so I won't bother you with it. It is sufficient to say what the change from classical Hamiltonian mechanics (which was equivalent to Newtonian mechanics) to quantum mechanics was all about.
The change was this: In quantum mechanics the action does not change in a continuous manner, but can take only discrete values. The step from one value to another is called the Planck constant. Fundamentally, this is the only difference between quantum mechanics and classical mechanics!
While quantum mechanics was developed, everybody knew that Hamiltonian mechanics is mathematically equivalent to Newtonian mechanics, so they assumed that once quantum mechanics was in place we could trace our tracks back to a Newtonian causal perspective. This would have allowed us to understand what we were actually talking about. But not so! Insofar nobody has discovered any such a causal perspective equivalent to the quantum mechanical formalism.
In a certain sense this implies that the Hamiltonian perspective is actually more fundamental than the Newtonian one even in classical mechanics. But no one really understands the Hamiltonian classical mechanics either! It was developed as a mathematical tool and it wasn't supposed to be taken seriously. But now it pops up everywhere from the general theory of relativity to statistical mechanics.
Let me give you a certain idea of how that tiny change of Hamiltonian mechanics, making the action a discrete quantity which isn't allowed to change continuously, could lead to so much weirdness. In classical (non-quantum) mechanics the state of something is given by its position and momentum (where it is and to where it's going and how fast and how difficult it is to change its motion). Suppose now that you couldn't fix the position and momentum exactly because fixing one parameter changes the other one at random. So, now - in quantum mechanics - the state of the system is located in a certain finite square (or rectangle), rather than being a certain point defined by a certain position and momentum. The minimum surface of this rectangle whithin which the state of the system is located is the Planck constant (the limit below which action cannot go).
Anyone who has played an old strategy game like Warcraft or Starcraft should understand what I'm now talking about: Remember when you told to one unit to go to some place and it ended up in some totally different place instead? Or remember when you were making a formation of several units neatly organized and when you were telling the entire formation to go to some place its whole organization broke apart? The reason why the programmers made the units move in such a crappy manner was that the map was discrete - instead of being continuous. Each unit occupied a certain, relatively large, square.
So when you told to a unit in place A to go to place B the game had to solve Hamilton's problem - it had to find, out of all the possible trajectories, the best one (for instance the one that takes the least amount of time). The reason why the program often failed in this task is that on a discontinuous map there is more than one solution to Hamilton's problem. Look at this image: there are several paths that have the exact same distance (measured in points). Hamilton's principle has no way of discerning between them. Interestingly, the paths between the ones highlighted by me are longer (although to the naked eye they may appear to be straighter).
In the same way, applying Hamilton's principle in quantum mechanics it doesn't lead to a single trajectory - like it used to in classical mechanics. It is more difficult to understand why this change leads to a break down of classical probability theory, but it can be shown mathematically. As if this was not enough, the issue of spin comes on top of it.
You can see why we can no longer switch from the Hamiltonian perspective (which looks to everything from the exterior and introduces a certain selection principle that acts on all the imaginable possibilities) to a Newtonian-like causal approach. There is nothing that pushes the particle to go on the blue path from A to B or that pushes it on the yellow path. Pure randomness decides whether it would go on one path or the other. Nonetheless, after the motion has happened it appears that some order still exists - no particle goes on the path between the two. In other words, although different particles go on different trajectories all of the trajectories share certain statistical properties. So, one is left puzzled: Assuming that the particles don't have any premonitions about their future on what grounds do they cherry pick their paths? We're describing them from a god's eye Hamiltonian perspective, but how do they do it? Nobody knows the answer to this question and that's why Feynman said nobody understands quantum mechanics.

 14 DAY TRIAL //
14 DAY TRIAL //