Newton's Gamble

Although most people have heard of Newton and have some vague clue about what he did, few actually think about motion in Newtonian terms. For some reason that escapes me, high school education seems to be incapable of sticking this discovery into people's heads. Most people learn about it and than forget it. It's impossible not to wonder whether they really ever learn about it. Maybe it's just an illusion that they learn about it, an illusion created by the fact that high school children manage to solve all those problems.

This matters because virtually all physical science and, consequently, all the technological advances shaping our everyday environment start with Newtonian mechanics. Not knowing what Newtonian mechanics and science, in general, is all about widens the gap between your self and your environment. Paradoxically, although our environment is becoming ever increasingly artificial, it also becomes increasingly mysterious. This paradox is the outcome of the lack of scientific culture.

In a previous article, I tried to describe the so-called "point" of Newtonian mechanics, the small discovery about force and motion spawning a great bulk of consequences. I did what probably all the high school teachers do, so maybe focusing on the apparently simple "seed" is not the way. Maybe focusing on the real subtleties of Newton's discovery will make this theory more mind grabbing. So, here it is.

Newton's theory is a huge and incredible gamble. It is incredible because, at first, nobody, not even Newton himself, thought it could be pushed very far. For example, Newton created his theory of mechanics and figured out a formula for the gravitational force. This formula for gravitation was devised in such a way as to produce the planetary orbits described by Kepler's laws. (These laws were deduced by Kepler using the very precise observations of Tycho Brache ? they were a concise way of putting together Brache's observations.) But then, Newton had to test his formula of gravitation on something else, in some place where it wasn't specially designed to work. So, he turned to the motion of the Moon around the Earth and used his formula to compute the distance between the Moon and the Earth.

His result was off track from the empiric observations of his day by a factor of ten. So, he abandoned his theory thinking it was just a coincidence that it managed to recreate Kepler's laws ? if the theory was to be truly a universal theory of gravitation it should have applied to the Moon as well. But several years later, new observations showed that the old data about the Moon were awfully wrong. The new data fitted the prediction of Newtonian theory exactly. So, Newton resurrected his theory.

But why was it so easy for him to think that his theory might be wrong? I think that this may be related to the reason why high school students so easily forget what the theory is all about. After three centuries of observations, we know that his theory is incredibly precise and we know that its limits (now described by the theory of relativity and by quantum mechanics) are quite esoteric. So physicists might tend to believe that Newtonian theory is a sure shot, once the idea crosses your head you know that reality must be like that. But it isn't a sure shot at all! On the contrary.

Thinking about motion

Galileo and Kepler observed motion and used math to record their observations in a synthetic form. But how about using math to think about motion caring less about observations?

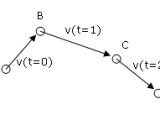
Let's suppose we want to determine the entire motion (the trajectory) of some thing. We are wondering: What do we need to know? The trajectory is a function that tells you what position the thing has at each moment in time. In other words, the trajectory is a table telling you: at time 0 the thing is in place A (having the coordinates such and such and such), at time 1 second, the thing is in place B, after 2 seconds it is at C, and so on. (If you want to trace the trajectory with increasing precision, for example with a time resolution of 1 millisecond instead of 1 second, you just need to add more lines in between ? instead of having a 5 lines table to describe a motion of 5 seconds, you have 5000 lines describing the same motion with increased resolution.)

Let's suppose we know where the thing is at time 0 and we want to determine where it will be at time 1. What do we need to know at time 0? Answer: we need to know how fast the thing is moving and in what direction ? in other words, we need to know its velocity, v(t=0). How about the position after 2 seconds? We need to know the velocity at moment 1, v(t=1). But what do we need to know at moment 0 so we could determine the velocity at moment 1? Answer: we need to know how fast its velocity is changing and in what direction it is changing ? in other words, we need to know its acceleration.

The same reasoning works ad infinitum: if you want to know the position after n seconds, you need to know n + 1 parameters at moment 0: the position, the velocity, the acceleration, the variation of acceleration and so on.

What I just described is called a Taylor series (or a Taylor expansion) ? it?s the idea that you can recreate a function (such as the trajectory), or a segment of a function, knowing a large number of parameters describing the function in just one single point (at one moment in time).

But, according to the Taylor reasoning, in order to know the entire trajectory, you need to know an infinite number of parameters! It seems a truly hopeless job. But here enters Newton. What Newton's second law of motion says is this ? and this is the huge gamble: It says that you can always deduce the acceleration (the second parameter in the Taylor series) if you know the position and the velocity (the first two parameters) of the thing.

This is quite a bold and unbelievable claim! Why should it be like that?! Could it really always be like that? This gamble, the Newtonian gamble, has always worked insofar, and not even relativity and quantum mechanics have changed that. And, as far as I'm aware of, nobody knows why this gamble works. Many physicists, including myself, rank this dilemma among the deepest mysteries we have.

How Newtonian mechanics works

In Newtonian mechanics you can always find a function, called force, which depends solely on position and velocity and you can express the acceleration with the help of this function. Thus, if you know this function ? if you know the force ? you know the acceleration. Then you can compute, by "differentiating" the function again and again, the next parameters in the Taylor series. After you have computed a sufficiently large number of parameters (given your goals, the desired precision) you can place them in the Taylor series and there you have the trajectory (the table that tells you where the thing will be at each subsequent moment of time).

Stripped down to the essentials, this is all that the scientists at NASA or ESA planning space travels do. They know the force ? the gravitational force and the spacecraft's thrust ? so they can compute the trajectory.

Newton's original gamble, the really big gamble, was that, in any situation, you can find the force ? that you can express the acceleration as a function depending solely on position and velocity. When Newton created his theory, he only knew of elastic force (that depends solely on position), of friction (that in general depends both on position and velocity) and of gravitation (that depends solely on position). From here to everything is a long way but it was (almost) covered in just three centuries.

Newtonian mechanics also incorporates two additional gambles that make the situation easier to handle mathematically. These two additional gambles can be gathered under the name of "reductionism". Both are used for a single purpose: for having the ability to make computations of complex situations based on the knowledge of very simple toy situations.

The two reductionist gambles are: 1) The idea that you can add forces in order to obtain a "resultant" force (this idea is equivalent to the idea that energy is conserved ? when two of more forces combine, no energy is lost or gained). 2) The idea that when thing A exerts a force on thing B, thing B exerts an opposite but equal force on thing A (this idea is equivalent to the idea that momentum is conserved).

The addition of forces allows us to find out experimentally (in very simple situations) the formulae for some "fundamental" forces and then use these formulae to make predictions in complex situations. Without the addition of forces, we would have to try to figure out the formula for the force in each new situation. Newton's second law tells us only that a formula for force should exist; but the addition of forces also tells us how to actually find that formula in each case, using the knowledge obtained in the simple toy situations (the "resultant", complex, force is just the sum of all the simple forces).

The conservation of momentum allows us to care less about what's happening inside a body and to take into consideration only the forces that act on the thing as a whole (the internal forces cancel each other due to this principle and we're left only with the forces that act upon the entire body).

How relativity works

The theory of relativity added an important twist to the story. In Newtonian mechanics, the trajectory is in three dimensions. But it was discovered that when things move at very high speeds, not all observers see the same trajectory. To me, and according to my watch, it might seem that the moving thing is in place A at moment 1, and in place B at moment 2, but to you, and according to your watch, it may seem, for instance, that it is in place B at moment 1 and place A at moment 2. But still, we're both watching the same thing!

To sort this out, one needs to consider the trajectory in space-time (as observed by you or me) and to index the motion based on the so-called proper time (the time measured by the thing itself). More on this here. But once one has the space-time idea in place, replacing the three-dimensional space, the entire Newtonian world-view (and its gambles) is kept in place.

How quantum mechanics works

At first, quantum mechanics seems to mark the destruction of the entire Newtonian gamble. Quantum phenomena don't even agree with the basic Taylor reasoning, because that reasoning is based on the concept of trajectory. The quantum stuff just doesn't seem to travel on trajectories. (According to the Heisenberg's principle, measuring the position very precisely disturbes the velocity, so you cannot even know how to get from A to B. How could you than create the entire trajectory?)

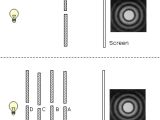
Here is a very simple experiment that proves this amazing fact about trajectories: We have a light bulb, a wall with a very tiny hole in it, and a screen behind the wall with the hole. When we turn on the light we see the image of the hole on the screen. However, we also see a number of increasingly fainter rings of light around the central image of the hole. This image of the hole together with the circles of light is called a diffraction pattern.

This pattern needs an explanation ? it seems that not all the photons (the particles of light) do the same thing under the same conditions ? some end up in the central spot but others end up in the outer diffraction rings. Any Newtonian would reason that this happens because the conditions are not properly specified ? not all the photons are ejected in the same way from the light bulb and some reach the hole from, say, an upward position and thus end up in a ring.

So, we add more walls with tiny holes in them in order to specify the conditions as perfectly as possible. Now, the path of the photons that are emitted by the light bulb and that eventually reach the screen is specified very well ? those photons have all passed through the tiny hole A, and B, and C, and so on.

There's a funny thing that happens when we add such walls: nothing. No matter how well we specify the path of the photons, the diffraction image on the screen remains unchanged ? photons keep reaching the outer rings with exactly the same probability as before (when only one wall was present).

According to the Newtonian gamble, only two walls should have been sufficient to determine the entire trajectory ? to make it unique ? because only two parameters are supposed to be needed. This simple experiment shows that in case of photons the Newtonian gamble fails miserably ? there is no force (a function depending only on position and velocity that could determine the acceleration and thus, via the Taylor expansion, a completely determined and unique trajectory).

But the fact that no matter how many holed walls you add nothing changes, also shows that the Taylor expansion itself fails (not only Newton's gamble). You may add even an infinite number of holed walls between the light bulb and the screen and you would still have the diffraction pattern intact.

However, this failure was short lived. It turns out that, although the concept of trajectory is not as general as Newton would have it, there is another way of specifying the "state" of a thing that is still in accordance to Newton's gambles. It turns out that although it is impossible to predict the actual trajectory of something, you can predict the probability distribution of various possible trajectories. And the mathematical object that helps you do this, called the amplitude of probability (or the wave function), obeys all three Newtonian gambles (the force is replaced by something called Hamiltonian).

In some cases, the probability distribution is as such that one particular trajectory is very probable and others are very improbable ? this is the case covered by the classical Newtonian mechanics when only one possible trajectory is assumed possible. But in other cases (such as the motion of photons), there are always a multitude of possible trajectories. Thus, the probabilistic view is more general and incorporates as a special case the classical Newtonian situation (which is deterministic).

How chaos theory works

The chaotic phenomena are the "enemy within" the classical Newtonian mechanics itself. It turns out that there are many cases ? even very simple ones ? when the Taylor expansion is made helpless by the very mathematical form of the forces. We use the forces to compute the higher terms in the Taylor expansion and we're doing this under the assumption that more terms we have, more precisely the trajectory will be determined ? but we also used to think that the first (the roughest) approximation is given by the first terms in the expansion.

However, it turns out that for some combinations of forces ? for example if we have three or more bodies interacting gravitationally, or if we have a pendulum oscillating in atmosphere and being pushed periodically by some force etc. ? the Taylor expansion ends up as such that the higher terms are larger than the first ones! This means that you cannot really use the Taylor expansion to approximate the trajectory. Or, in other words, any small disturbance in position or in velocity at time zero can lead to a very different trajectory ? there are large differences after some period of time.

Until recently, physicists have assumed, without worrying too much about the issue, that in Newtonian mechanics, all the trajectories come grouped together ? that if two trajectories are close to each other (both from the point of view of position and of velocity) at some moment in time, they will always be close to each other. But this is not so.

If you think about it, this situation is kind of weird ? the mathematical formulas of the forces have been created under the Taylor reasoning, but now, when you assume them to be correct, you conclude that the Taylor reasoning doesn't always work. Although the situation in chaos theory isn't yet entirely clarified, it seems that it is possible to still save the Newtonian gambles in the same way as they have been saved in quantum mechanics: switching from the trajectory perspective to a probabilistic one.

So, the situation today is that we know that the original Newtonian gamble works incredibly well, although it has some limitations highlighted by relativistic and by quantum phenomena, but we have no idea why it works so well. We also know that the challenges posed by relativity and by quantum phenomena have been surpassed in a way that preserves the spirit of the Newtonian gambles, most importantly reductionism. However, the idea of trajectory is no longer as fundamental as it once has been and it seems to be only a special case in the framework of the probabilistic thinking. The inside challenge posed by the discovery of chaotic phenomena, which are intrinsic even to the classic Newtonian mechanics, might be the only serious dilemma. They certainly raise all sorts of unexpected questions that don't fit very well with the type of thinking behind the Newtonian gambles.