We are all too familiar with the pressure to conform to the majority and to the temptation of doing so. But sometimes it pays off to be in the minority. In fact, each time there is a competition for some limited resources, the winner is the one that stands out from the crowd. In such situations, in order to win, you have to be in the minority.
One of the hottest scientific topics right now studies precisely how "agents" behave in such a game. And the consequences are remarkably far reaching. The minority game is defined as a game with a large number of players, N, each player having to make at each round of the game a choice between A or B. After all players have made their choice the ones that happened to be in the minority (that have chosen the least win one point.
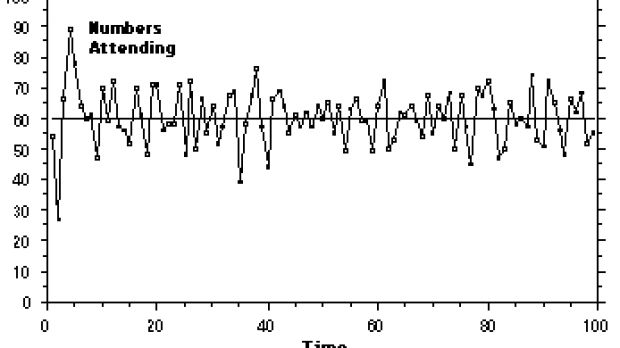
The original version of the game was invented by W. Brian Arthur of the Santa Fe Institute and involved a choice between going to the El Farol bar or staying at home. It was assumed that if more than 60% of the population goes to the bar it would be so overcrowded that all the fun was lost. But how could one know in advance whether or not the bar would be overcrowded? The image shows the bar attendance in the first 100 weeks as modeled by some simple theory of inductive decision making.
Arthur had used this example to draw attention to a certain paradox of deductive reasoning - of the idea that there always exists a "best solution" that can be determined by logic. The El Farol problem cannot have a standard, generally agreed, "rational" solution. There cannot be one strategy, the best strategy, that everyone can use. If everyone uses the same strategy for deciding whether or not to go to the bar the bar will be either full or empty each night. Everyone would lose all the time.
Thus, in such situations, when the resources are limited and it pays off to be a minority, there can be only a diversity of individual solutions, of individual strategies of tackling the problem. If somehow a single method for dealing with the situation is imposed everyone loses.
Almost ten years ago, Damien Challet and Yi-Cheng Zhang have taken the El Farol problem and applied it to financing. Since then, the new field of "econophysics" has sparked a lot of attention. In the Challet and Zhang financing game, the choice between A and B does not involve going to a bar but selling or buying stock. When one makes financial speculations one has to buy before everybody is crowding to buy (thus driving the price up) and to sell before everybody starts selling (thus driving the price down). Thus, the big winners are always managing to be part of the minority.
There has been a lot of interest in developing the mathematics of this game. The reason for this interest is not only practical, physicists trying to get rich, but also theoretical. The models have yielded surprising features showing under which conditions cooperation appears spontaneously in a group, and the field also proved to be a generalization of the type of game theory simulations modeling the Darwinian evolution.
"If we look into the [economic] literature, as a physicist one may get the strange feeling that the Theory is so detached from the Experiments," Zhang wrote in an essay for the Europhysics News. "On the one hand the Theory is extremely refined and self-consistent with little effort to compare with empirical evidence; on the other the experiments (e.g. traders' activities) are also extensively performed with little reference to the Theory. It is revealing to see how Soros, one of the top players in finance considers the Theory [G. Soros, Alchemy of Finance]."
"In short, current prevailing theory assumes equilibrium, the descriptions are mostly static. Little is said how an equilibrium can be attained, if attainable at all," he added. "Dynamics of markets can be found nowhere. Meanwhile, Insight gained in the statistical mechanics, especially in non-equilibrium processes, may inspire physicists to have a try in formulating a sort of dynamical theory for some economical processes."
The Minority Model
One of the most surprising features of the minority model is how much one can obtain with so little. The model has only three basic parameters: the number of players, N, the average memory span the players have about their own actions, M, and the number S of possible strategies the players can employ to guide their actions. A particular strategy is simply a mathematical function that takes into account what has happened in the past M rounds of the game (the personal successes or failures of being part of the minority) and suggests what should be done in the present round (what choice A or B should be taken).
To this, one can furthermore add an evolutionary twist to the game by allowing the parameters to change from round to round. The least successful players will not have any offspring, while the most successful will clone themselves. The clone would not inherit the exact strategies or the same memory span (but one varied at random up or down), thus mimicking the idea of a random mutations.
Moreover, one can add another complication to the game: the players might use not only their own personal experience but also take into consideration the available public information.
"We carry out localized deductions based on our current hypotheses and act on them. And, as feedback from the environment comes in, we may strengthen or weaken our beliefs in our current hypotheses, discarding some when they cease to perform, and replacing them as needed with new ones. In other words, where we cannot fully reason or lack full definition of the problem, we use simple models to fill the gaps in our understanding. Such behavior is inductive," Arthur wrote in his original paper on the El Farol problem. "This type of behavior may not be familiar in economics. But we can recognize its advantages. It enables us to deal with complication: we construct plausible, simpler models that we can cope with. It enables us to deal with ill-definedness: where we have insufficient definition, our working models fill the gap. It is not antithetical to 'reason,' or to science for that matter. In fact, it is the way science itself operates and progresses."
How many strategies are there?
One can ask: If one agent has a certain memory span M, how many possible strategies are available to her? At first, the number, T, of all possible strategies seems to grow extremely fast as the memory span increases. If M is 3, there are 8 possible strategies. If M is 10, T is 1 with 300 zeros after it! A number that is "infinite for all practical purposes", as Zhang put it.
However, it turns out that not all these possible strategies are independent of each other. Some strategies are related to others via simple logical relations. For one thing, half of the strategies are saying the exact opposite of the other half. Moreover, many strategies give the same results. The number, K, of independent strategies is much smaller than T.
For each player, we draw from this pool of all the possible strategies, a number of S strategies. The agent would choose what strategy to use from one of these S strategies that are available to her. So, if there are N players, there is a number of N times S available strategies to the players.
Three phases
Physicists talk about certain changes, called phase transitions that are characterized by the fact that small variations of some of the system's properties cause a dramatic change to the system as a whole. For example, as one gradually increases the temperature from below zero to above zero water turns from ice into liquid. If one gradually decreases the pressure liquid water starts to boil and turns to vapors.
It turns out that the group of agents playing the minority game also experiences such phase transitions as one gradually changes some of its properties, N, M or S. The system has three phases.
In the first phase the agents have such short memories that the number, K, of strategies available to each individual is very small relative to the number of all the available strategies in the group (the product NS). This means that the agents would necessarily employ many similar strategies. But because they all choose more or less the same thing they fall into the El Farol paradox of deductive reasoning every time - they all lose. They are too dumb to invent a large diversity of strategies and they behave like the proverbial sheep going off the cliff.
The other extreme is when they have such large memories that, given how many they are (or how few they are, actually), their strategies virtually never meet. This means that the each individual in the group is behaving in a random, unconstrained way.
The middle phase is the most interesting one. This is the case when the product NS, describing the total number of available strategies, is approximately equal to K. The agents can now both employ effective strategies and have to avoid each others' strategies. It turns out that, on the average, when the game is played for a sufficiently long time, all the agents win. This phase corresponds to the appearance of cooperation. In a certain sense, this is a very simple model of how the division of labor spontaneously appears in a group: each individual stabilizes on a certain strategy (or a small number of strategies) instead of going a random through all of them, and this helps the others. Each individual wins by being in a minority of its own.
One also gets the same result when turns the minority game into an evolutionary game: "Adaptation puts an evolutionary pressure on the players' strategies," Zhang wrote, "they tend to be as diversified as possible."
It's hard not to think of the similarity between these three phases and the classical solid, gas and liquid phases, but the connection is only superficial. The transition between, say, solid and liquid involves something called latent heat. This means that some of the system's properties, such as the temperature, "wait" for the whole transition to take place before changing. In the minority game there is actually only one phase transition, that happens near the point where NS = K, and this transition is continuous. The interesting middle state is actually a transitory state between the two extreme phases.
Instead of varying M (and implicitly K) one can also get from one phase to the other by varying S, how many strategies each individual is allowed to choose from, or N, the number of individuals. The first state is dominated by the "herding effect" and everyone loses, the last one is dominated by extreme individualism and random behavior, and the middle one is the cooperative state in which agents constrain each other and organization appears spontaneously. What is spectacular is that all this can appear in a rather rudimentary mathematical model!
Doing the evolution
"We would like to let the population to evolve to this cooperative region without imposing the fixed parameters," Zhang wrote. "To this end we introduce another level of adaptation by adding the Darwinism to this competition game. Worst player is periodically wed out of the game; best player is allowed to produce an offspring. The new born player is a clone copy of his parent with the virtual capital reset to zero. A small mutation rate is assumed to ensure genetic diversity, i.e. one of his inherited strategies is replaced. The total population is kept constant without loss of generality. The newly drawn strategy can have its M changed by one unit. This permits the players to find the best suitable M."
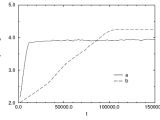
The graph shows how M has evolved in time in two different populations (a: N = 101, b: N= 1001). (Credit: Challet and Zhang.) The number of strategies S was taken to be 5. It is interesting to note that in the larger population it took longer for the adaptation to happen and the equilibrium value for M was also larger - individuals need bigger brains to cope with a larger society.
This type of evolution is more complex than the standard type of evolution biologists describe. The selfish gene model assumes that the individual doesn't have a choice for what strategy to employ - the animal is a robot that is simply acting the program encoded in its genes and favored by the environmental conditions. The genes and the environment combine to determine in a causal manner what strategy the animal "chooses".
One can recover this standard biological model by setting the number S = 1. In that case one gets the classic selfish gene idea: the competition is not so much between the individuals as it is between the strategies themselves (or the genes that contain the information about these strategies).
Non-ergodicity
Ergodicity (or non-ergodicity) is a property that characterizes the group as a whole. One can look at a certain moment in time and see what strategies are employed or can look at a certain individual and see what strategies uses as times goes by. If the two perspectives, the momentary group picture and the individual's journey, are statistically equivalent the group is ergodic.
Ergodicity is thus a kind of homogeneity of the dynamic evolution of the group. The two extreme states are both ergodic because, statistically, the agents are all doing the same things. But as the group approaches that middle state where cooperation exists, and, as noted, in the evolutionary variant of the game the group naturally tends toward that state, the ergodicity breaks.
At the individual level, the non-ergodicity of the group means that the reliability of one's own experience is diminished. The behavior of the group simply doesn't fit very well with the each individual's behavior.
In physics, the non-ergodic systems, certain types of glasses, have a rather strange property: the older they are the harder it is to erase their memory of the past - what happened to them gets stored. But J.A.F. Heimel and A. De Martino have shown that this does not hold in case of the minority game. The group of agents does not store its history properly, on the contrary. This is probably due to the fact that the system is made of agents rather than of causal entities, but this is just a speculation. No one really understands yet why this difference exists. But considering the fact that the minority game can be used to model certain human activities this offers an explanation of why the past isn't recorded in human societies as well as the non-ergodicity of the human ensemble might have suggested and as well as we might want.
Another interesting consequence of the non-ergodicity in the minority game was discovered by Tobias Galla and David Sherrington. They have showed that this makes the group very sensitive to initial conditions. Although the dynamics of the group can be predicted in the ergodic states, it cannot be determined when non-ergodicy takes hold. If one uses the minority game to model economic realities this obviously becomes important.
 14 DAY TRIAL //
14 DAY TRIAL //